Principal component analysis (PCA) - Lundquist Urban Ecology Lab

Principal Component Analysis (PCA) is a statistical technique used to reduce the dimensionality of a data set while retaining as much of the variation in the data as possible. It does this by finding a new set of uncorrelated variables, called principal components, which can be used to represent the original data.

To perform PCA in R, the first step is to load the data and scale it if necessary. Next, the prcomp() function can be used to perform the analysis, which returns an object containing the principal component scores and loadings. The summary() function can be used to view the results, and the biplot() function can be used to create a graphical representation of the data in the new principal component space.

Here is an example of performing PCA in R:

	# Running a principal components analysis (PCA) in R

	# Load data
	data(iris)

	# Remove factors
	data <- iris

	# Scale data
	data_scaled <- scale(data[–5])

	# Perform PCA
	pca_results <- prcomp(data_scaled, scale = TRUE)

	# View results
	summary(pca_results)

	# Create biplot
	# library(devtools)
	# install_github("vqv/ggbiplot")
	library(ggbiplot)
	g <- ggbiplot(pca_results, choices=c(1,2), obs.scale = 1, var.scale = 1, groups = iris$Species, ellipse = TRUE)
	g <- g + geom_point(aes(color = iris$Species), size = 3)
	g <- g + theme_classic()
	g <- g + scale_color_discrete(name = 'Species', labels = c("I. setosa", "I. versicolor", "I. virginica"))
	g <- g + theme(legend.direction = 'horizontal', legend.position = 'top')
	print(g)

view raw pca.r hosted with ❤ by GitHub

PCA in R

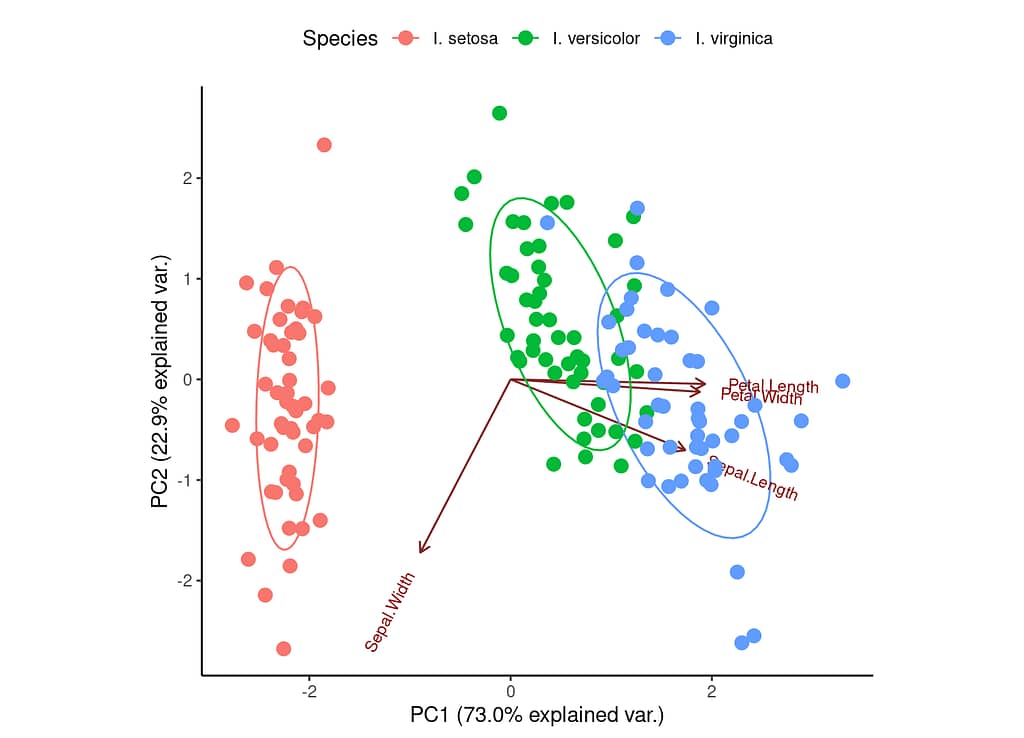
You can see that the first principal component (PC1) explains 73% of the variance in the data. The next principal component (PC2) explains an additional 22.9%. The ellipses represent potential groupings of data based on the principal components. In the example above, we can see that the Iris species form three relatively clear clusters (particularly I. setosa).

We can do something similar in Python:

	# Running a principal components analysis (PCA) in Python
	#%%

	import pandas as pd
	# pip install scikit-learn
	from sklearn.decomposition import PCA
	import matplotlib.pyplot as plt
	import seaborn as sns


	# Import data
	url = "https://raw.githubusercontent.com/lundquist-ecology-lab/biostatistics/main/example_data/iris.csv"
	data = pd.read_csv(url)

	# Scale data
	from sklearn.preprocessing import StandardScaler
	scaler = StandardScaler()
	data_scaled = scaler.fit_transform(data.iloc[:,[0,3]])

	# Perform PCA
	pca = PCA(n_components=2)
	pca.fit(data_scaled)

	# Project data onto first two principal components
	data_pca = pca.transform(data_scaled)

	# Plot PCA
	sns.scatterplot(x=data_pca[:, 0], y=data_pca[:, 1], hue=data['Species'], palette='Set1')
	plt.xlabel("First Principal Component")
	plt.ylabel("Second Principal Component")
	plt.show()
	# %%

view raw pca.py hosted with ❤ by GitHub

PCA in Python

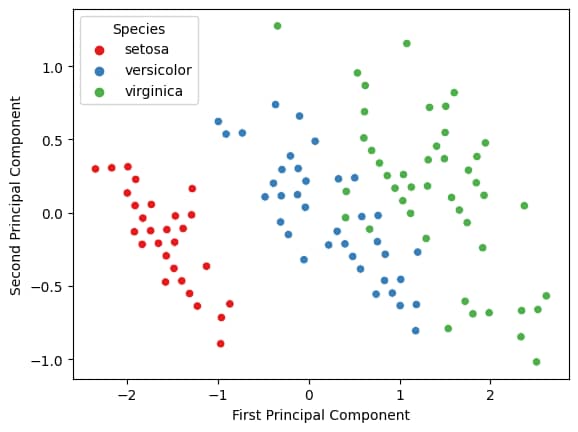
You might notice that there is a lot more information provided in the R plot, but more importantly, the results are the same for both PCAs, regardless of which programming language we use.